Vedang Asgaonkar At the curtain of the waterfall
Publications
Generator Assisted Mixture of Experts For Feature Acquisition in Batch
Vedang Asgaonkar, Aditya Jain, Abir De
AAAI-24 accept, arxiv
We deal with a feature acquisition task for classification. Primarily, we are given an initial subset of features, which is used to decide a new subset of features to be queried. Unlike prior work, this is done in a batch setting, new features are queried simultaneously instead of sequentially. This implies that the new features to be queried can only be conditioned on the set of initial features. Subsequently, we perform classification based on the availble feature values. We propose GENEX, an algorithm for deciding which subset of features to query under a budget constraint on the number of features that can be queried.
Salient Features
- We propose a greedy algorithm to decide the set of features to be acquired on the training set
- We utilize Locality Sensitive Hashing to enable quick retrieval of the optimal feature subset during inference
- We construct a mixture of experts model to perform the classification task on a heterogenous domain of feature subsets
- We utilize a generator to produce a subset of the features that are to be acquired. This reduces the number of queries that need to be performed to the oracle set of features.
- We provide theoretical backing and experimental verification to our greedy algorithm
Problem Setup
We use \(x \in \mathbb{R}^n\) to denote a feature vector and \(y\) to denote the classification label. We denote \(\mathcal{I} = [n]\) as the set of feature indices, \(\mathcal{O} \subset \mathcal{I}\) as the set of intial observed features and \(\mathcal{U} \subset \mathcal{I} \setminus \mathcal{O}\) as the set of features to be acquired by the algorithm. We make use of a generator, which produces generates a subset \(\mathcal{V} \subset \mathcal{U}\) of the features to save on querying cost. The remaining features in \(\mathcal{U} \setminus \mathcal{V}\) are queried. We use \(p(x'[\mathcal{V}]\vert x[\mathcal{O}])\) as a stochastic generator. The classifier is denoted by \(h(\bullet)\). Then, the overall optimization objective is
\[loss(h,p,U,V\vert O) = \mathbb{E}_{x'[V] \sim p(\bullet\vert x[O])} l(h(x[O \cup U \setminus V] \cup x'[V]))\] \[min_{h,p,V_i,U_i} \sum_{i \in D} loss(h,p,U_i,V_i\vert O_i)\]subject to the budget constraint \(\vert U_i \setminus V_i \vert \le q_{max}\) for each point \(i \in D\), the dataset.
Proposed Approach
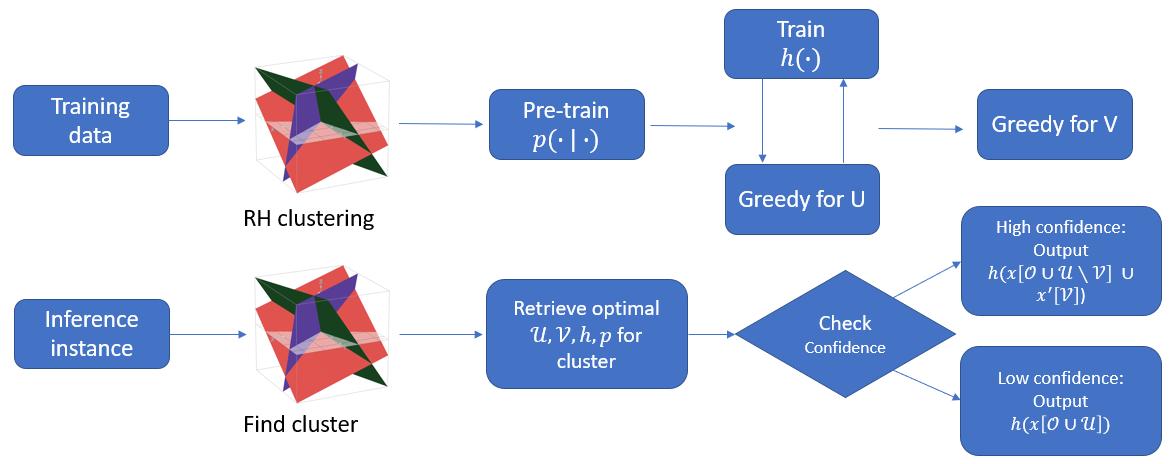
Data Partitioning
To reduce the amount of heterogeneity in feature subsets available for classification, we cluster the data using the value of observed features \(x[\mathcal{O}]\). We perform random hyperplane (RH) based clustering, which provides good bucket balance and per-instance objective as opposed to k-means and gaussian mixture clustering.
We further use the data partitions to reduce the number of optimization variables. This is done by assigning the same optimal \(\mathcal{U}, \mathcal{V}\) for data points in the same bucket. Moreover, the optimal value of \(\mathcal{U}, \mathcal{V}\) is determined by a greedy algorithm on the training set. During inference, we simply locate the cluster corresponding to the test instance, and use the optimal \(\mathcal{U}, \mathcal{V}\) for that cluster. This helps reduce the time complexity for identifying the subset during inference to simply that or retrieval i.e. logarithmic in the number of clusters.
Mixture Models
We deploy mixture models on the partitioned data by training an independent classifier for each cluster. This helps deal with the heterogeneity in feature spaces as well as reduce inter-instance coupling of the optimal \(\mathcal{U}\) and \(\mathcal{V}\) subsets.
Training and Greedy Algorithm
We first pretrain the generator to model arbitrary conditionals on the data in a \(\beta\)-VAE style. We then alternate between training the classifier and a step of constructing the optimal \(\mathcal{U}\) greedily. To that end, we construct a surrogate objective which is a function of \(\mathcal{U}\), decoupling it from \(\mathcal{V}\).
\[F(h,p,U\vert O) = \Delta(U) l(h(x[O \cup U]), y) + (1-\Delta(U)) l(h(x[O] \cup x'[U]), y)\]The objective \(F(h,p,U\vert O)\) is a linear combination of the loss from using oracle values for \(\mathcal{U}\) and generating the full subset \(\mathcal{U}\), weighted by the uncertainty of the generator \(\Delta(U)\). The greedy algorithm greedily adds elements to \(\mathcal{U}\) while the surrogate objective decreases.
We subsequently employ a greedy algorithm to construct \(\mathcal{V} \subset \mathcal{U}\). This algorithm greedily adds elements from \(\mathcal{U}\) to \(\mathcal{V}\) while the overall objective decreases.
Inference
During inference, the test instance is clustered using \(x[\mathcal{O}]\). The optimal \(\mathcal{U}, \mathcal{V}\) subsets and the classifier \(h\) for this cluster will be used subsequently. The generator is used to generate \(x'[\mathcal{V}]\) conditioned on \(x[\mathcal{O}]\). We also query the values of \(x[\mathcal{U} \setminus \mathcal{V}]\). Then, we perform classification using \(h(x[\mathcal{O} \cup \mathcal{U} \setminus \mathcal{V}] \cup x'[\mathcal{V}])\). If the confidence of the classifier is low, we subsequently query \(x[\mathcal{V}]\) and classify using \(h(x[\mathcal{O} \cup \mathcal{U}])\).
Results
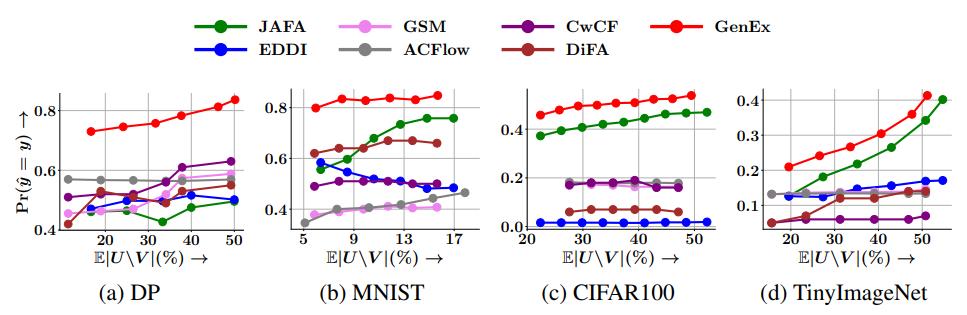
We plot accuracy v/s query cost for four datasets, compare GENEX against a variety of RL based and greedy baselines. Our experiments show a significant gain in accuracy as compared to state-of-the-art methods.
Contacts
For any questions/suggestions, please contact Vedang Asgaonkar, Aditya Jain and Abir De